트리와 쿼리
문제
간선에 가중치와 방향성이 없는 임의의 루트 있는 트리가 주어졌을 때, 아래의 쿼리에 답해보도록 하자.
- 정점 U를 루트로 하는 서브트리에 속한 정점의 수를 출력한다.
만약 이 문제를 해결하는 데에 어려움이 있다면, 하단의 힌트에 첨부한 문서를 참고하자.
입력
트리의 정점의 수 N과 루트의 번호 R, 쿼리의 수 Q가 주어진다. (2 ≤ N ≤ 105, 1 ≤ R ≤ N, 1 ≤ Q ≤ 105)
이어 N-1줄에 걸쳐, U V의 형태로 트리에 속한 간선의 정보가 주어진다. (1 ≤ U, V ≤ N, U ≠ V)
이는 U와 V를 양 끝점으로 하는 간선이 트리에 속함을 의미한다.
이어 Q줄에 걸쳐, 문제에 설명한 U가 하나씩 주어진다. (1 ≤ U ≤ N)
입력으로 주어지는 트리는 항상 올바른 트리임이 보장된다.
출력
Q줄에 걸쳐 각 쿼리의 답을 정수 하나로 출력한다.
문제풀이
tree의 구조를 잘 알고 있어야 풀 수 있다.
tree는 노드(vertex)의 개수가 n개, edge의 개수가 n-1 개인 그래프이다.
모든 노드는 이어져 있고, cycle이 존재하지 않는다.
문제를 보자마자 재귀적으로 풀면 되겠다고 생각했다.
루트부터 시작해서 루트 노드의 서브 트리의 개수는 루트 노드 바로 아래 노드의 서브 트리의 개수들의 합 + 자기자신(1) 이다.
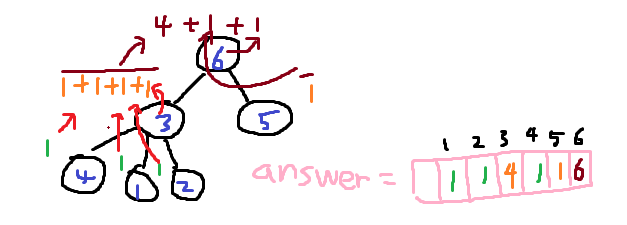
서브 트리는 자기 자신도 포함한다는 것을 잊지 말자.
위와 같은 개념을 반복하면 쉽게 풀 수 있다.
루트 노드의 서브 트리의 개수의 합을 구하려면 그 서브트리의 서브트리의 개수의 합을 구하면 된다. 재귀적으로 leaf노드에 도달할 때 까지 반복해주어 모든 노드의 서브트리의 개수를 구한 뒤 알맞게 출력해주면 답이다.
#include <iostream>
#include <vector>
using namespace std;
int answer[100001];
int visited[100001];
int n, r, q;
vector<int> edges[100001];
void Dfs(int node) {
visited[node] = 1;
answer[node] = 1;
// 자신의 자식 노드의 서브트리들의 개수의 합
for(int i=0; i<edges[node].size(); i++) {
if(visited[edges[node][i]] == 0) {
Dfs(edges[node][i]);
answer[node] += answer[edges[node][i]];
}
}
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> n >> r >> q;
for(int i=0; i<n-1; i++) {
int a, b;
cin >> a >> b;
edges[a].push_back(b);
edges[b].push_back(a);
}
Dfs(r);
for(int i=0; i<q; i++) {
int a;
cin >> a;
cout << answer[a] << "\n";
}
return 0;
}다른 사람들의 풀이를 보니, 부모 노드는 반드시 하나이기 때문에 visited를 쓰지 않고 매개변수로 부모 노드일 경우만 제외하는 식으로 해도 된다.
edges 배열+벡터도 그냥 2중 벡터로 해줘도 된다. 단, 이중 배열은 공간을 너무 차지하기 때문에 하지 않는다.
'알고리즘(Algorithm)' 카테고리의 다른 글
| [C++] 최소 힙 (1927번) (0) | 2022.11.23 |
|---|---|
| [C++] 단어 뒤집기2 (17413번) (0) | 2022.11.22 |
| [C++] 감시 피하기 (18428번) (0) | 2022.11.19 |
| [C++] 마법사 상어와 비바라기 (21610번) (0) | 2022.11.14 |
| [C++] 퇴사 (14501번) (0) | 2022.11.14 |




