| 2 초 | 512 MB | 64502 | 17211 | 8322 | 21.688% |
문제
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선이 같은 위치를 갖는다. 아래 그림은 N = 5, H = 6 인 경우의 그림이고, 가로선은 없다.
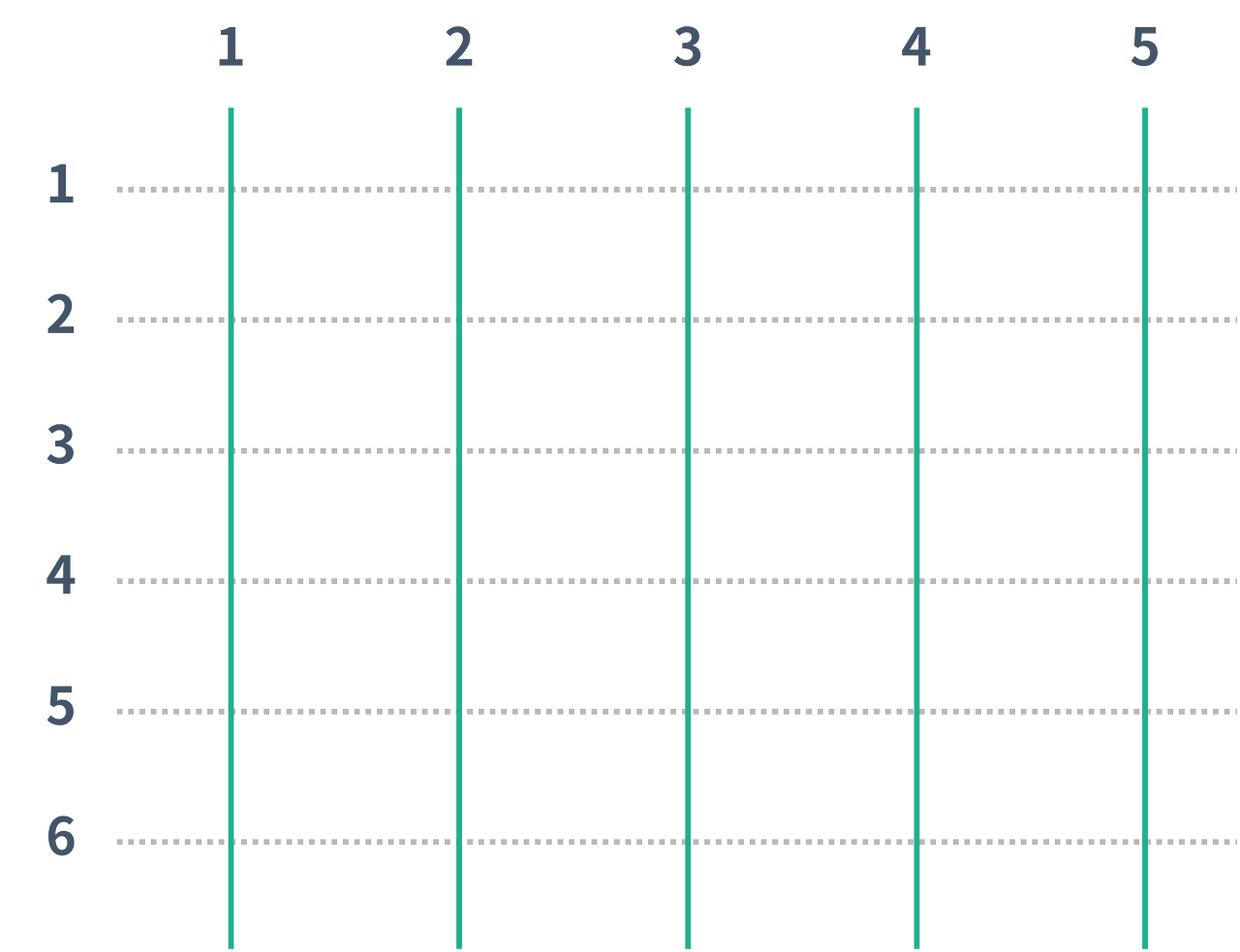
초록선은 세로선을 나타내고, 초록선과 점선이 교차하는 점은 가로선을 놓을 수 있는 점이다. 가로선은 인접한 두 세로선을 연결해야 한다. 단, 두 가로선이 연속하거나 서로 접하면 안 된다. 또, 가로선은 점선 위에 있어야 한다.
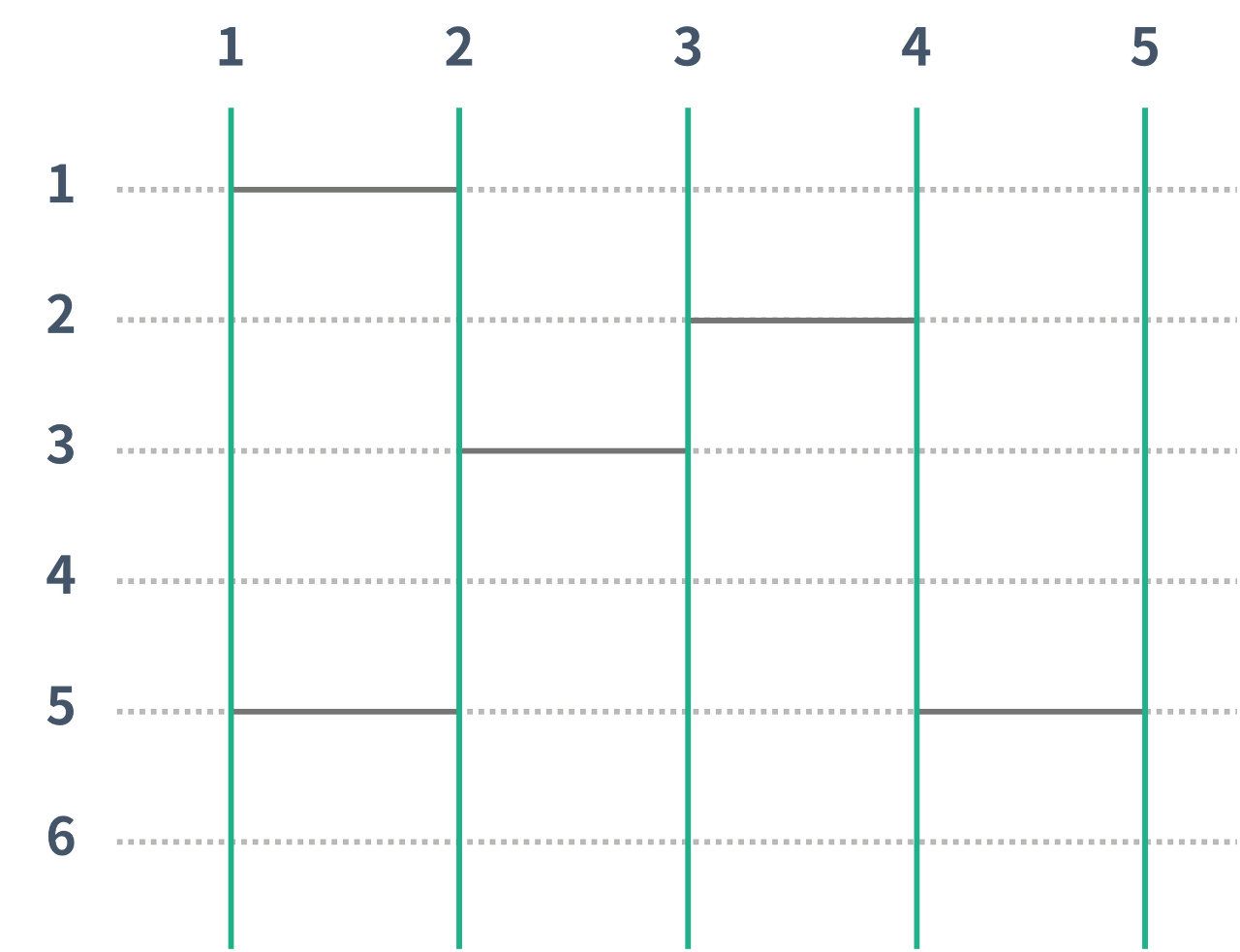
위의 그림에는 가로선이 총 5개 있다. 가로선은 위의 그림과 같이 인접한 두 세로선을 연결해야 하고, 가로선을 놓을 수 있는 위치를 연결해야 한다.
사다리 게임은 각각의 세로선마다 게임을 진행하고, 세로선의 가장 위에서부터 아래 방향으로 내려가야 한다. 이때, 가로선을 만나면 가로선을 이용해 옆 세로선으로 이동한 다음, 이동한 세로선에서 아래 방향으로 이동해야 한다.
위의 그림에서 1번은 3번으로, 2번은 2번으로, 3번은 5번으로, 4번은 1번으로, 5번은 4번으로 도착하게 된다. 아래 두 그림은 1번과 2번이 어떻게 이동했는지 나타내는 그림이다.
| 1번 세로선 | 2번 세로선 |
사다리에 가로선을 추가해서, 사다리 게임의 결과를 조작하려고 한다. 이때, i번 세로선의 결과가 i번이 나와야 한다. 그렇게 하기 위해서 추가해야 하는 가로선 개수의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 세로선의 개수 N, 가로선의 개수 M, 세로선마다 가로선을 놓을 수 있는 위치의 개수 H가 주어진다. (2 ≤ N ≤ 10, 1 ≤ H ≤ 30, 0 ≤ M ≤ (N-1)×H)
둘째 줄부터 M개의 줄에는 가로선의 정보가 한 줄에 하나씩 주어진다.
가로선의 정보는 두 정수 a과 b로 나타낸다. (1 ≤ a ≤ H, 1 ≤ b ≤ N-1) b번 세로선과 b+1번 세로선을 a번 점선 위치에서 연결했다는 의미이다.
가장 위에 있는 점선의 번호는 1번이고, 아래로 내려갈 때마다 1이 증가한다. 세로선은 가장 왼쪽에 있는 것의 번호가 1번이고, 오른쪽으로 갈 때마다 1이 증가한다.
입력으로 주어지는 가로선이 서로 연속하는 경우는 없다.
출력
i번 세로선의 결과가 i번이 나오도록 사다리 게임을 조작하려면, 추가해야 하는 가로선 개수의 최솟값을 출력한다. 만약, 정답이 3보다 큰 값이면 -1을 출력한다. 또, 불가능한 경우에도 -1을 출력한다.
문제풀이
가로선을 0개 추가한 뒤 정답인지 확인하고, 1개 추가한 뒤 정답인지 확인하고, 2개 추가한뒤 정답인지 확인하고, 3개 추가한뒤 정답인지 확인한다.
주의할점은 가로선 추가의 중복을 없애주는 것이다. 이 작업을 해주지 않으면 시간초과가 난다. 내가 그랬다.
r 을 보면, 0부터 시작하는게 아니라 이전에 추가한 가로선 r 부터 다시 돈다. 이렇게 해야 중복을 줄일 수 있다.
그런데 난 이래도 612ms 가 나온다. 정답자들 코드를 보면 0ms 만에 되는데 어떻게 이렇게 줄일 수 있는지는 정말 모르겠다.. 그래서 유일하게 달라보이는 로직을 참고해서 적용했더니 4ms 까지 줄었다.
반복 순서 바꾸고, while문 하나 넣었다고 왜이렇게 결과가 달라진것일까??? 저게 뭐길래?
자기 자신의 왼쪽, 오른쪽 모두 사다리가 존재하지 않다면, 다음 가로선으로 이동하는 로직이다.
사다리를 한 번 설치하고 나면, 이후에 이미 설치된 사다리가 나올 때 까지의 빈칸은 고려해줄 필요가 없다. 진짜 이게 이해가 안됐는데 아래 참고 블로그를 보고 이해가 되었다.

빨간색 선을 추가해서 이미 dfs를 돌렸다면 그 아래 다른 사다리가 나오기 전까지 또 돌려볼 필요가 없는것이다. 왜냐하면 빨간색 선을 추가한 것과 정확히 같은 행위를 하기 때문이다. 이렇게 하면 dfs 반복 행위를 엄청나게 줄일 수 있다.
#include <iostream>
using namespace std;
int n, m, h;
int arr[30][10];
int answerCheck;
bool isAnswer() {
for(int col=0; col<n; col++) {
int now_col = col;
for(int row=0; row<h; row++) {
if(arr[row][now_col] == 1) now_col++;
else if(now_col-1>=0 && arr[row][now_col-1] == 1) now_col--;
}
if(now_col != col) return false;
}
return true;
}
void dfs(int now_cnt, int cnt, int r) {
if(answerCheck) return;
if(now_cnt == cnt) {
if(isAnswer()) {
answerCheck = 1;
cout << cnt;
}
return;
}
// for(int i=r; i<h; i++) {
// for(int j=0; j<n; j++) {
// if(j != 0 && arr[i][j-1] == 1) continue;
// if(j != n-1 && arr[i][j+1] == 1) continue;
// if(arr[i][j] == 1) continue;
// arr[i][j] = 1;
// dfs(now_cnt+1, cnt, i);
// arr[i][j] = 0;
// }
// }
for(int j=0; j<n; j++) {
for(int i=0; i<h; i++) {
if(j != 0 && arr[i][j-1] == 1) continue;
if(j != n-1 && arr[i][j+1] == 1) continue;
if(arr[i][j] == 1) continue;
arr[i][j] = 1;
dfs(now_cnt+1, cnt, i);
arr[i][j] = 0;
while((j>=0 && !arr[i][j-1]) && (j<n && !arr[i][j+1])) i++;
}
}
}
int main() {
ios::sync_with_stdio(0); cin.tie(NULL); cout.tie(NULL);
cin >> n >> m >> h;
for(int i=0; i<m; i++) {
int a, b;
cin >> a >> b;
arr[a-1][b-1] = 1;
}
for(int i=0; i<4; i++) {
dfs(0, i, 0);
}
if(!answerCheck) cout << -1;
return 0;
}
'알고리즘(Algorithm)' 카테고리의 다른 글
| [C++] 낚시왕 (17143번) (1) | 2023.10.14 |
|---|---|
| [C++] 나무 재테크 (16235번) (0) | 2023.10.13 |
| [C++] 2048 (Easy) (12100번) (1) | 2023.10.10 |
| [C++] 마법사 상어와 파이어볼 (20056번) (0) | 2023.10.09 |
| [C++] 상어 중학교 (21609번) (1) | 2023.10.08 |


